Кусок пластилина сталкивается скользящим том направлении

Кусок пластилина сталкивается скользящим том направлении

Рекомендуем! Лучшие курсы ЕГЭ и ОГЭ

Задание 29. Кусок пластилина сталкивается со скользящим навстречу по горизонтальной поверхности стола бруском и прилипает к нему. Скорости пластилина и бруска перед ударом направлены противоположно друг другу и равны = 15 м/с и = 5 м/с. Масса бруска в 4 раза больше массы пластилина. Коэффициент трения скольжения между бруском и столом = 0,17. На какое расстояние переместятся слипшиеся брусок с пластилином к моменту, когда их скорость уменьшится на 30%?

Выберем ось X, сонаправленную со скоростью бруска. По закону сохранения импульса в проекции на ось X:

, (1)

где m — масса пластилина, u — скорость слипшихся тел после соударения. По закону изменения механической энергии при торможении тел:

. (2)

Объединяя (1) и (2), получим:

м.

Источник

Решения задач ЕГЭ

С4. К источнику тока с ε = 12 В и внутренним сопротивлением r = 2 Ом подключён реостат, сопротивление которого может изменяться в пределах от R min = 1 Ом до R max = 10 Ом. При какой силе тока в реостате выделяется максимальная полезная мощность?

1. Рассмотрим источник тока с заданной величиной ЭДС ε и внутренним сопротивлением r нагруженный на внешнее сопротивление R. На внешнем сопротивлении будет выделяться активная электрическая мощность N а

2. Для выяснения величины максимально возможной активной мощности N a(max) будем изменять величину внешнего сопротивления до величины R m . Математически это означает определение экстремума функции N a =f(R) путём её дифференцирования по сопротивлению и приравнивания производной к нулю, стандартная процедура нахождения экстремума функции:

2. Так как R и r всегда положительные величины, то условие выполняется при r = R m . Мощность, выделяемая во внешней цепи, достигает возможно большего значения при равенстве внутреннего источника тока и внешнего сопротивления. Сила тока в этом режиме составит

I = 2 ε r = 12 4 = 3А;

С5. Идеальный LC-контур состоит из конденсатора С = 20 мкФ и катушки с индуктивностью L = 8 мГн. Амплитуда колебаний силы тока i m = 6 мА. Какова максимальная энергия электрического поля конденсатора?

С6. Работа выхода электрона из фотокатода А = 4,5 10 − 19 Дж. Какова максимальная скорость фотоэлектронов при облучении фотокатода светом с длиной волны λ = 375 нм?

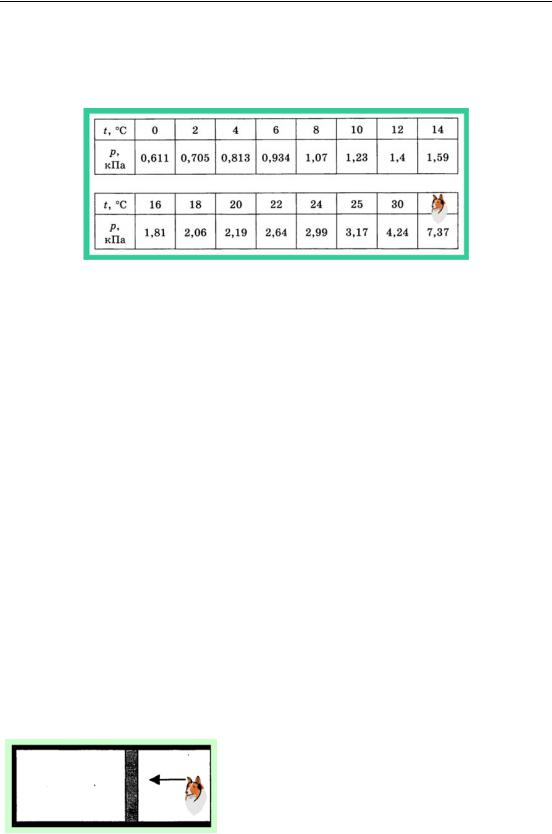
С1. Человек в очках вошёл с улицы в тёплую комнату и у него запотели очки. Температура воздуха в комнате t 1 = 18 0 C, относительная влажность ϕ = 0,5. Какова была температура на улице?

1. Относительная влажность воздуха:

; p = p H ϕ ; p H ≈ 2,06кПа; р ≈ 1,03кПа; t 2 ≈ 8 0 C;

С2. Мяч бросают вертикально вверх со скоростью v 0 = 20 м/с. Какой путь пройдёт мяч за τ = 3 с движения? Сопротивлением воздуха пренебречь .

1. Время подъёма мяча в высшую точку траектории и высота подъёма h 1 ;

Поскольку мяч летит τ = 3 с, а поднимается в течение t 1 = 2 c, то в тече-

нии времени t 2 = τ − t 1 = 1 c мяч будет свободно падать

Путь, пройденный за время τ :

S = h 1 + h 2 = 25 м;

С3. В горизонтальном теплоизолированном цилиндрическом сосуде под поршнем при комнатной температуре находится ν = 0,5 моль гелия. Поршню сообщают скорость v = 8 м/с, направленную влево. Масса поршня m = 1 кг. На сколько изменится температура гелия

Рис. 19.3. Горизонтальный поршень к моменту остановки поршня?

С4. Цилиндрическая катушка диаметром D = 0,1 м состоит из однослойной обмотки медного провода (ρ = 1,7 10 −8 Ом м) диаметром d = 10 − 4 м. По обмотке пропускают постоянный ток силой I = 10 А. Какое количество электричества Q протечёт через обмотку при замыкании её концов?

1. В начальном состоянии переключатель находится в положении 1, т.е. через обмотку протекает постоянный ток, сечение катушки пронизывает постоянный по величине и направлению магнитный поток. При переводе переключателя в положение

2 сила тока, вследствие наличия в цепи ин- Рис. 19.4. Количество электричества дуктивности L исчезает не мгновенно, а по

i = Ie − ( RL ) t ,

где R − активное сопротивление, t − время, в течение которого величина тока изменяется от I до 0.

2. Количество электричества Q за время t определится как

3. Подставим в уравнение Q значение силы тока i, с учётом того, что при t =

∞ сила тока стремится к нулю, а при t =0 сила тока составляет I

4. Подставляя пределы интегрирования, получим:

5. Запишем далее уравнения индуктивности и активного сопротивления катушки

где ρ − удельное сопротивление, l 0 − длина проводника, s 0 − сечение провода, d − диаметр, N − число витков соленоида, l s − длина обмотки, s s − сечение катушки.

6. Подставим уравнения индуктивности и активного сопротивления в уравнение количества электричества

= μ N 2 π D 2 π d 2

Q I 0 0 4 l s 4 ρl 0 .

7. Выразим длину катушки через её диаметр и число витков

8. Подставим длину катушки в уравнение (7)

Q = μ 0 N 2 π D 2 d 2 π I = μ 0 π Dd 2 I .

16 l s ρπ DN 16 ρl s

9. Отношение длины катушки к числу витков равно диаметру катуш-

40 10 − 7 0,1 10 − 4 10

С5. Идеальный колебательный контур состоит из конденсатора С = 20 мкФ и катушки индуктивности L= 8 мГн. Амплитуда колебаний заряда на конденсаторе q m = 8 нКл. Какова максимальная энергия магнитного поля катушки?

С6. Работа выхода электрона из фотокатода А = 4,5 10 − 19 Дж. Каков максимальный импульс фотоэлектронов при облучении фотокатода светом с длиной волны λ = 375 нм?

С1. Относительная влажность воздуха в комнате ϕ = 55%, температура t 1 = 18 0 С. На сколько градусов должна понизится температура воздуха на улице, чтобы оконные стёкла запотели?

; p = ϕ p H = 0,55 2,066 ≈ 1,14кПа;

t 2 ≈ 9 0 C; t = 18 − 9 = 9 0 C;

С2. Кусок пластилина сталкивается со скользящим в том же направлении по горизонтальной поверхности стола бруском и прилипает к нему. Скорость пластилина v 1 = 10 м/с скорость бруска v 2 = 5 м/с. Масса бруска в 3 раза больше массы пластилина. Коэффициент трения между бруском и столом μ = 0,48. На какое расстояние переместится брусок с прилипшим к нему пластилином к моменту, когда их скорость уменьшится на ζ = 25%?

1. Скорость движения бруска с пластилином:

2. Закон сохранения энергии для движущейся в присутствии силы трения системы:

+ μ 4mgL x ; v 3 2 − 0,75v 3 2 = 2 μ gL x ; L x =

С3. Аэростат, нерастяжимая оболочка которого имеет объём V = 200 м 3 , наполняют горячим воздухом с температурой Т 1 = 553 К при нормальном атмосферном давлении при температуре окружающего воздуха Т 0 = 373 К. Какую максимальную массу М должна иметь оболочка, чтобы шар начал подниматься. В нижней части оболочки имеется отверстие.

1. Плотность холодного и тёплого воздуха:

Рис. 20.3. Аэростат

2. Условие нарушения равновесия шара:

Mg ≤ ( ρ 0 −ρ x ) gV;

M ≤ ( ρ 0 −ρ 1 ) V ≈ 130 кг;

С4. В плоском конденсаторе диэлектрик между пластинами вследствие увеличения влажности стал пропускать ток. При плотности тока j = 0,02 А/м 2 в диэлектрике ежесекундно выделялось ζ = 10 Дж/м 3 теплоты. Чему равна напряжённость электрического поля в конденсаторе?

1. Количество теплоты, выделяющееся в проводнике:

Q = ζ V τ = IU τ = jsEd τ ; E =

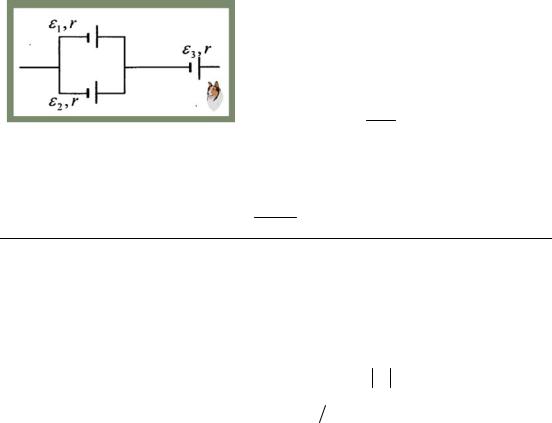
С5. Определить эквивалентную ЭДС и эквивалентное внутренне сопротивление соединения источников тока.

1. Эквивалентное внутреннее сопротивление определится как сумма двух параллельных и одного последовательного резистора одинакового сопротивления:

Рис. 20.5. Соединение источников r Σ = r r + r r + r = 1,5r;

2. Параллельно соединённые источники обладают одинаковым внутренним сопротивлением, поэтому эквивалентная ЭДС определится в виде алгебраического среднего:

ε Σ = ε 1 + 2 ε 2 + ε 3 ;

С6. С какой скоростью вылетает α-частица из радиоактивного ядра, если она, попадая в магнитное поле с индукцией В = 2 Тл перпендикулярно силовым линиям, движется по окружности радиуса r = 1 м?

1. Условие нахождения α -частицы с зарядом q α = 2e на круговой орбите:

q α vB = m α v 2 ;

μ = 4 10 − 3 кг моль;

N A ≈ 6 10 23 моль − 1 ;

2. Скорость α -частицы:

10 − 19 2 1 6 10 23

С1. Относительная влажность воздуха в комнате ϕ = 63%, а температура t 1 = 18 0 C. На сколько градусов должна понизиться температура воздуха на улице, чтобы оконные стёкла запотели?

p = ϕ p H = 0,63 2,066 ≈ 1,3кПа;

≈ 11 0 C; t = 18 − 11 = 7 0 C;

С2 . На нити висит груз массой m. Нить отвели на угол α 0 и отпустили. Найти силу

натяжения нити Т, как функцию угла α. В каких точках траектории вектор ускорения груза перпендикулярен направлению нити?

1. Исследуем энергетическое состояние груза в двух положениях: при отклонении на максимальный угол α 0 и а произвольном положении нити, когда угол отклонения от положения статического равновесия составляет α . Уравнение закона сохранения энергии в этом случае представится следующим образом

где K 2 − кинетическая энергия в положении

Рис. 21.2. Натяжение нити

груза II, U 1 − потенциальная энергия груза в

2. Геометрическая сумма силы тяжести

и натяжения нити F , всегда

совпадает с направлением скорости, т.е. A = 0

3. Запишем второй закон Ньютона в проекции на направление нити подвеса

F = mgsin α ; F i = mgcos α ; mgsin α = ma n ;

T − mgcos α = mv L 2 ;

4. Величина натяжения нити будет являться функцией угла отклонения, т.е. будет зависеть, в конечном счёте, от текущего значения высоты h

h = Lcos α − Lcos α 0 = L ( cos α − cos α 0 ) ;

5. Образуем систему из трёх уравнений с тремя неизвестными величинами

h = L ( cos α − cos α

T − mgcos α = m2gL ( cos α − cos α 0 ) ;

T = 2mg ( cos α − cos α 0 ) + mgcos α ;

T = mg ( 2cos α − 2cos α 0 + cos α ) = mg ( 3cos α − 2cos α 0 ) ;

6. Вектор ускорения шарика будет перпендикулярен при α = α 0 . Максимальное натяжение нити будет в нижней точке траектории. Отклоним нить на

угол α 0 = 90 о и отпустим, в этом случае: cos α 0 = 0 , в нижней точке траектории при α = 0 о

7. При круговом вращении груза он может находиться на круговой траектории при условии

при этом закон сохранения энергии представится следующим образом

т.е. потенциальная энергия в верхней точке траектории равна кинетической энергии в момент прохождения грузом самой нижней точки траектории.

Уравнение второго закона Ньютона в нижней точке траектории примет вид

T max = mg + mv L 2 = mg + 4mg = 5mg ;

С3. На сколько отличается внутренняя энергия воздуха, заполняющего зал объёмом V = 249 м 3 зимой и летом, если летом температура в зале достигает Т 1 = 27 0 С, а зимой падает до Т 2 = 17 0 С при одинаковом нормальном давлении р 0 10 5 Па? Молярную массу воздуха принять равной μ = 29 10 − 3 кг/моль.

1. Летом и зимой а комнате будет разное количество воздуха:

p 0 V = ν 2 RT 2 ;

ν = p 0 V ; 1 RT 1

2. Внутренняя энергия летом и зимой:

C4. Квадратная проволочная рамка расположена в одной плоскости с длинным прямолинейным проводником так, что две её стороны параллельны проводу. По рамке и проводу текут токи одинаковой силы I = 1 кА. Определить силу F А , действующую на рамку, если ближайшая к проводу сторона рамки находится на расстоянии, равном её длине.

1. В виду симметрии взаимного расположения длинного проводника и квадратной рамки линии действия равнодействующих сил Ампера F 2 , F 4 совпадают, а направлены они в противоположные стороны, другими словами,

2. На вертикальные стороны рамки так же будут действовать силы F 1 , F 3 ,

линии действия которых совпадают, а направлены они в противоположные стороны. Таким образом, сила, действующая на рамку со стороны магнитного поля проводника, определится в виде геометрической суммы векторов

F Σ = F 1 + F 2 + F 3 + F 4 , | F Σ | = F 1 − F 3 .

3. Индукция магнитного поля проводника определится уравнениями

B 1 = 4 μ π 0 d I ( cos α 1 − cos α 2 ) , B 3 = 4 μ π 0 2 I d ( cos α 1 − cos α 2 ) ,

в данном случае α 1 → 0 0 , α 2 → 180 0 , поэтому

Источник

Кусок пластилина сталкивается скользящим том направлении

Добрый день. Объясните пожалуйста, почему в законе сохранения импульса не учтено, что к изначальной скорости снаряди прибавляется скорость от энергии взрыва. Иными словами, почему в правой части уравнения суммарный импульс после взрыва (после прибавления энергии), а в левой части импульс до взрыва, т.е. без доп. энергии взрыва.

Потому что есть два разных закона сохранения: закон сохранения импульса и закон сохранения энергии. Разберемся последовательно.

Полная механическая энергия системы в данном случае не сохраняется, поскольку взрыв совершает работу по разгону осколков. То есть энергия взрыва (по сути внутренняя энергия взрывчатого вещества) приводит к увеличению полной механической энергии системы.

Для выполнения же закона сохранения полного импульса системы необходимо только, чтобы на систему не действовали внешние силы. Взрыв происходит «изнутри», он отталкивает два куска друг от друга, это внутренняя сила, импульс сохраняется.

Простой пример: пусть есть два куска пластилина равной массы, вы их кидаете навстречу друг друга с одинаковой скоростью. Ясно, что они слипнутся, и получившийся комок останется на месте. Кинетическая энергия кусков пропала, а импульс, как был, так и остался равен нулю.

Спасибо, теперь всё понятно. Т.е. в подобных задачах изменение энергии учитывается только в законе сохранения энергии, а в импульсах не учитывается. Я правильно понимаю?

Я полагаю, что во всех задачах, а не только в этой, не нужно смешивать две величины: импульс и энергию. Тогда будет все правильно.

Просто каждый раз надо отслеживать, выполняется ли тот или иной закон сохранения. Система может получать импульс из вне (если ее кто-то пинает), может получать или терять энергию, просто надо быть аккуратным в понятиях, тогда ждет успех 🙂

Здравствуйте! Подскажите, пожалуйста, зачем нужно начальную массу обозначать 2m? Просто m чем хуже?

Ничем 🙂 Так захотел автор решения 🙂

Доброго времени суток.

Прощу прощения, но возник некий казус у меня при решении данной задачи. Полностью солидарна с Вами с первой половиной решения, действовала так же, однако далее, при выраженной скорости сразу начала подставлять в исходное уравнение и получила отличный от здешнего ответ — 1МДж. Несколько раз перерешивала, всё то же.

Затем решила подставить исходные даннные в Вашу конечную формулу и удивилась- получается-то 1 МДж.

Посмотрите внимательнее, в решении через обозначена масса осколка, то есть нужно подставлять 2 кг, а не 4 кг.

В результате получается ответ, как указано здесь.

«суммарная кинетическая энергия осколков увеличилась на величину dE», почему же вы dE приписываете к начальной кинетической энергии до разрыва?в чем моя ошибка?у меня получилось — (-5 МДж). помогите пожалуйста)

Все верно, если к начальной кинетической энергии прибавить , то как раз и получится новая, большая энергия. Можно наоборот, из новой вычесть и получить начальную. Результат, естественно будет тот же самый.

С Новым Годом! 🙂 Вы не мо­же­те объяснить, по­че­му в за­ко­не сохранения энер­гии не учи­ты­ва­ет­ся потенциальная энергия? (ведь сна­ряд и оскол­ки находятся на высоте)

Она не изменяется. Да и вообще, начало отсчета можно поместить в точку взрыва.

Решение правильное, но если смотреть реально, то масса снаряда должна уменьшиться, так как взрыв, приведший к возрастанию энергии, произошел за счет уменьшения массы снаряда. А это значит, что говорить, будто снаряд массой 4 кг разделился на 2 осколка по 2 кг каждый, неверно.

При взрыве происходит химическая реакция. При таких реакциях выделяется энергия и, действительно, это выделение энергии обуславливает изменение массы, но это изменение массы настолько мало, что его можно не учитывать.

Вычисляем, подставляя значения из условия: дельта Е = 4(900-400)(900-400) =

4*500*500=1000000 Дж=1 МДж

Снаряд массой 4 кг, летящий со скоростью 400 м/с, разрывается на две равные части, одна из которых летит в направлении движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличилась на величину Определите скорость осколка, летящего по направлению движения снаряда.

Введем обозначения: — масса снаряда до взрыва; — модуль скорости снаряда до взрыва; — модуль скорости осколка, летящего вперёд; — модуль скорости осколка, летящего назад.

Система уравнений для решения задачи:

Выразим из первого уравнения: и подставим во второе уравнение. Получим:

Ответ:

я согласен с вашем ответом там действительно получается 900 м/с но при вашем решение где в корне вы делите дельта Ек на m такой ответ не получается поскольку у вас там 2m:2= m a m=4 а 500000:4=125000 а там корень не извлекается , и зачем вы берёте 2m я не пойму ведь там по ясно написано что снаряд 4 кг а при деление на две равные части получается 4:2=2 при таком раскладе ответ верный а при вашей там не так

Там в самой первой строчке сказано, что обозначает массу осколков, а — массу снаряда. Поэтому .

При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н (см. рисунок).

На краю трамплина скорость гонщика направлена под углом к горизонту. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящийся на той же высоте, что и край трамплина. Какова высота полета h на этом трамплине? Сопротивлением воздуха и трением пренебречь.

Модель гонщика — материальная точка. Считаем полет свободным падением с начальной скоростью направленной под углом к горизонту. Высота полета определяется из выражения Модуль начальной скорости определяется из закона сохранения энергии так что При получаем

Ответ: высота подъема

напишите пожалуйста поподробнее,как вы нашли высоту h (никак не пойму)

В решении задачи используется формула для максимальной высоты полета тела, брошенного под углом к горизонту. При этом скорость вылета с трамплина определяется из закона сохранения полной механической энергии велосипедиста.

Напомню, как можно вывести формулу для высоты. При свободном падении тела, брошенного под углом к горизонту, вертикальная координата в системе отсчета, в которой начало отсчета помещено на уровне броска, определяется следующим образом (здесь — начальная скорость тела):

Приравняв это выражение нулю, можем найти время полета тела:

.

Время подъема равно времени спуска, следовательно для него имеем: .

Максимальная высота — это вертикальная координата в конце подъема, следовательно,

.

Про закон сохранения энергии: приравнивается полная механическая энергия на вершине склона (велосипедист обладает только потенциальной энергией, отсчитываем ее от уровня трамплина) и на уровне трамплина (велосипедист имеет только кинетическую энергию).

Есть альтернативное решение, в котором первую формулу можно не помнить. Просто выпишем два закона сохранения энергии. Первый между моментом старта и моментом отрыва от трамплина:

.

Второй: между моментом старта и моментом, когда велосипедист находится в максимальной точке полета. В этой точке он обладает и потенциальной, и кинетической энергией. При этом его скорость в этот момент времени направлена горизонтально. Как известно, при свободном падении тела, горизонтальная скорость его не изменяется, значит, скорость велосипедиста в максимальной точке равна . Следовательно необходимый нам закон сохранения энергии имеет вид

.

Решая систему из двух уравнений, получаем ответ.

Можете пояснить («разжевать») что значит следующее предложение в условии задачи:

«гонщик приземляется на горизонтальный стол, находящийся на той же высоте, что и край трамплина».

Что значит «на горизонтальный стол» ?

Какую информацию можно извлечь из этого предложения для решения задачи, или же это лишняя информация ?

В принципе, это не несет никакой смысловой нагрузки. Автор задачи просто попытался словесно описать картинку, которая прилагается к задаче. Если бы место, куда прыгает гонщик, вело бы себя как-то «холмисто», то было бы трудно задать вопрос: высота полета была бы не совсем точно определенной величиной. На его месте я бы, может, спросил: «На какую высоту подскочит велосипедист после отрыва от трамплина?» Тогда «горизонтальный стол» можно и не упоминать. 🙂

При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н (см. рисунок).

На краю трамплина скорость гонщика направлена под углом к горизонту. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящийся на той же высоте, что и край трамплина. Какова дальность полета L на этом трамплине? Cопротивлением воздуха и трением пренебречь.

Модель гонщика — материальная точка. Считаем полет свободным падением с начальной скоростью направленной под углом к горизонту. Дальность полета определяется из выражения

Модуль начальной скорости определяется из закона сохранения энергии

так что При получаем

Ответ: дальность полета

Критерии оценки выполнения задания

Приведено полное правильное решение, включающее следующие элементы:

1) верно записаны формулы, выражающие физические законы, применение которых необходимо для решения задачи выбранным способом;

2) проведены необходимые математические преобразования и расчеты, приводящие к правильному числовому ответу, и представлен ответ (включая единицы измерения). При этом допускается решение «по частям» (с промежуточными вычислениями).

Представленное решение содержит п. 1 полного решения, но и имеет один из следующих недостатков:

— в необходимых математических преобразованиях или вычислениях допущена ошибка;

— необходимые математические преобразования и вычисления логически верны, не содержат ошибок, но не закончены;

— не представлены преобразования, приводящие к ответу, но записан правильный числовой ответ или ответ в общем виде;

решение содержит ошибку в необходимых математических преобразованиях и не доведено до числового ответа.

Представлены записи, соответствующие одному из следующих случаев:

— представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на решение задачи, и ответа;

— в решении отсутствует ОДНА из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи;

в ОДНОЙ из исходных формул, необходимых для решения задачи (или утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла.

Источник