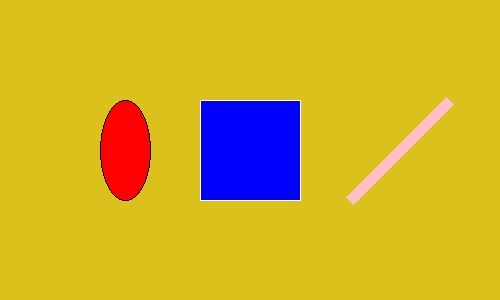Рисование линий алгоритм окружность

Алгоритмы взяты из прекрасной книги
П.В.Вельтмандер «Машинная графика»

Во многих областях приложений, таких как, например, системы автоматизированного проектирования машиностроительного направления, естественными графическими примитивами, кроме отрезков прямых и строк текстов, являются и конические сечения, т.е. окружности, эллипсы, параболы и гиперболы. Наиболее употребительным примитивом, естественно, является окружность. Один из наиболее простых и эффективных алгоритмов генерации окружности разработан Брезенхемом.

1 Алгоритм Брезенхема
Для простоты и без ограничения общности рассмотрим генерацию 1/8 окружности, центр которой лежит в начале координат. Остальные части окружности могут быть получены последовательными отражениями (использованием симметрии точек на окружности относительно центра и осей координат).

Окружность с центром в начале координат описывается уравнением:

X 2 + Y 2 = R 2

Алгоритм Брезенхема пошагово генерирует очередные точки окружности, выбирая на каждом шаге для занесения пиксела точку растра P_i(X_i, Y_i), ближайшую к истинной окружности, так чтобы ошибка:

E_i(P_i) = (X_i 2 + Y_i 2 ) — R 2

была минимальной. Причем, как и в алгоритме Брезенхема для генерации отрезков, выбор ближайшей точки выполняется с помощью анализа значений управляющих переменных, для вычисления которых не требуется вещественной арифметики. Для выбора очередной точки достаточно проанализировать знаки.

Рассмотрим генерацию 1/8 окружности по часовой стрелке, начиная от точки X=0, Y=R.

Проанализируем возможные варианты занесения i+1-й точки, после занесения i-й.

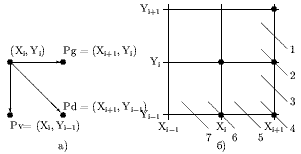
При генерации окружности по часовой стрелке после занесения точки (X_i, Y_i) следующая точка может быть (см. рис. 0.1а) либо Pg = (X_i+1, Y_i) — перемещение по горизонтали, либо Pd = (X_i+1, Y_i-1) — перемещение по диагонали, либо Pv = (X_i, Y_i-1) — перемещение по вертикали.

Для этих возможных точек вычислим и сравним абсолютные значения разностей квадратов расстояний от центра окружности до точки и окружности:

| Dg |

=

| (X+1) 2

+

Y 2

—

R 2 |

| Dd |

=

| (X+1) 2

+

(Y-1) 2

—

R 2 |

| Dv |

=

| X 2

+

(Y-1) 2

—

R 2 |

Выбирается и заносится та точка, для которой это значение минимально.

Выбор способа расчета определяется по значению Dd. Если Dd 0, то диагональная точка вне окружности. Это варианты 5-7. И, наконец, если Dd = 0, то диагональная точка лежит точно на окружности. Это вариант 4. Рассмотрим случаи различных значений Dd в только что приведенной последовательности.

Случай Dd

Здесь в качестве следующего пиксела могут быть выбраны или горизонтальный — Pg или диагональный — Pd.

Для определения того, какой пиксел выбрать Pg или Pd составим разность:

di

=

| Dg | — | Dd | =

| (X+1) 2 + Y 2 — R 2 | — | (X+1) 2 + (Y-1) 2 — R 2 |

И будем выбирать точку Pg при di Ј 0, в противном случае выберем Pd.

Рассмотрим вычисление di для разных вариантов.

Для вариантов 2 и 3:

Dg і 0 и Dd

di = (X+1) 2 + Y 2 — R 2 + (X+1) 2 + (Y-1) 2 — R 2 ;

Добавив и вычтя (Y-1) 2 получим:

di = 2 ·[(X+1) 2 + (Y-1) 2 — R 2 ] + 2·Y — 1

В квадратных скобках стоит Dd, так что

di = 2 ·(Dd + Y) — 1

Для варианта 1:

Ясно, что должен быть выбран горизонтальный пиксел Pg. Проверка компонент di показывает, что Dg Случай Dd > 0

Здесь в качестве следующего пиксела могут быть выбраны или диагональный — Pd или вертикальный Pv.

Для определения того, какую пиксел выбрать Pd или Pv составим разность:

si

=

| Dd | — | Dv | =

| (X+1) 2 + (Y-1) 2 — R 2 | — | X 2 + (Y-1) 2 — R 2 |

Если si Ј 0, то расстояние до вертикальной точки больше и надо выбирать диагональный пиксел Pd, если же si > 0, то выбираем вертикальный пиксел Pv.

Рассмотрим вычисление si для разных вариантов.

Для вариантов 5 и 6:

Dd > 0 и Dv Ј 0, так как диагональный пиксел вне, а вертикальный либо вне либо на окружности.

si = (X+1) 2 + (Y-1) 2 — R 2 + X 2 + (Y-1) 2 — R 2 ;

Добавив и вычтя (X+1) 2 получим:

si = 2 ·[(X+1) 2 + (Y-1) 2 — R 2 ] — 2·X — 1

В квадратных скобках стоит Dd, так что

si = 2 ·(Dd — X) — 1

Для варианта 7:

Ясно, что должен быть выбран вертикальный пиксел Pv. Проверка компонент si показывает, что Dd > 0 и Dv > 0, причем si > 0, так как диагональная точка больше удалена от окружности, т.е. по критерию si > 0 как и в предыдущих случаях следует выбрать вертикальный пиксел Pv, что соответствует выбору для вариантов 5 и 6.

Случай Dd = 0

Для компонент di имеем: Dg > 0 и Dd = 0, следовательно по критерию di > 0 выбираем диагональный пиксел.

С другой стороны, для компонент si имеем: Dd = 0 и Dv Ј 0 также выбираем диагональный пиксел.

Dd Ј 0 — выбор горизонтального пиксела Pg

di > 0 — выбор диагонального пиксела Pd

si Ј 0 — выбор диагонального пиксела Pd

si > 0 — выбор вертикального пиксела Pv

выбор диагонального пиксела Pd.

Выведем рекуррентные соотношения для вычисления Dd для (i+1)-го шага, после выполнения i-го.

1. Для горизонтального шага к X_i+1, Y_i

2. Для диагонального шага к X_i+1, Y_i-1

3. Для вертикального шага к X_i, Y_i-1

В Приложении 5 приведена подпрограмма V_circle, реализующая описанный выше алгоритм и строящая дугу окружности в первой четверти. Начальная инициализация должна быть:

Dd = (X+1) 2 + (Y-1) 2 — R 2 = 1 + (R-1) 2 — R 2 = 2*(1 — R)

Пикселы в остальных четвертях можно получить отражением. Кроме того достаточно сформировать дугу только во втором октанте, а остальные пикселы сформировать из соображений симметрии, например, с помощью подпрограммы Pixel_circle, приведенной в Приложении и заносящей симметричные пикселы по часовой стрелке от исходного.

В Приложении приведены подпрограмма V_BRcirc, реализующая описанный выше алгоритм и строящая дугу окружности во втором октанте с последующим симметричным занесением пикселов. Эта процедура может строить и 1/4 окружности. Подробнее см. текст Приложения. Там же приведена более короткая подпрограмма, строящая 1/8 окружности методом Мичнера [], (том 1, стр. 152). Остальная часть окружности строится симметрично.
0.15 Приложение 4. Процедуры генерации окружности

В данном приложении помещены процедуры генерации окружностей по алгоритму Брезенхема и Мичнера, а также программа T_Circle для тестирования данных процедур.

Источник

Рисуем геометрические фигуры в Python с помощью Pillow

Модуль ImageDraw из библиотеки обработки изображений Pillow (PIL) предоставляет методы для рисования круга, квадрата и прямой линии в Python.

Содержание статьи

Создание объекта Draw в Python

Используя объекта Image мы создадим фоновое изображение на которой мы будем рисовать наши фигуры при помощи объекта Draw . Не забудьте импортировать модуль Image и ImageDraw в начале кода.

Здесь создается пустое изображение с размером 500 на 300 пикселей и с тёмно желтым фоном.

Рисуем фигуры в Pillow: ellipse, rectangle и line

Вызываем методы рисования из объекта Draw для рисования фигур на нашем желтом фоне.

Рисуем эллипс, прямоугольник и прямую линию в качестве примера.

Справочник по параметрам методов рисования

Даже если, способы рисования отличаются в зависимости от используемого метода, следующие параметры являются общими для всех.

Область рисования — xy

Параметр xy указывает прямоугольную область для рисования новой фигуры.

Уточняется один из следующих форматов:

(((Верхняя левая x координата, Верхняя левая y координата), (нижняя правая x координата, нижняя правая y координата)) ;

(Верхняя левая x координата, Верхняя левая y координата, нижняя правая x координата, нижняя правая y координата) .

В методах line() , polygon() и point() используются многочисленные координаты вместо двух точек, представляющих прямоугольную область.

Метод line() рисует прямую линию, которая связывает каждую точку, polygon() рисует многоугольник, а метод point() рисует точку в 1 пиксель для каждой указанной точки.

Параметр fill — заполняем фигуру определенным цветом

Параметр fill указывает какой цвет будет использован для заполнения нашей геометрической формы.

Спецификация формата цвета отличается в зависимости от указанного режима изображения (объект Image ):

RGB : Указывает значение цвета в форме (R, G, B) ;

L (Черно-белое): Указывает значение (0-255) как целое число).

Значение по умолчанию None (не заполнено).

Есть три способа указать цвет, возьмем красный цвет, его можно записать так:

текстовый формат: red;

CSS формат (Шестнадцатеричный): #FF0000

RGB: (255, 0, 0)

Стоит учесть тот факт, что текстовый формат не имеет все цвета, кол-во доступных цветов ограничено в коде самой библиотеки. Вот весь список: https://github.com/python-pillow/Pillow/blob/8.1.0/src/PIL/ImageColor.py#L148

Лучше всего использовать шестнадцатеричный формат #FFFFFF (белый).

Параметр outline — цвет границ

Параметр outline указывает на цвет границы фигуры.

Спецификация формата цвета такая же, как и у параметра fill которого мы обсуждали выше. Значение по умолчанию равно None (без границ).

Параметр width — размер границ

Вне зависимости от рисуемой фигуры, вы можете указать размер в пикселях для границы фигуры.

Рисование эллипса и прямоугольника в Python

Эллипс (Круг): ellipse(xy, fill, outline) ;

Прямоугольник (Квадрат): rectangle(xy, fill, outline) .

Метод ellipse() рисует эллипс, область рисования указывается в параметр xy . Если мы зададим четыре координата которые будут соответствовать квадрату, то у нас получится ровный круг.

Источник

Читайте также: Рисование планшетом bamboo one